Quelques sous-groupes
du groupe du Rubik's cube

- " What's yellow and equivalent to the Axiom of Choice ?
- " Zorn's Lemon "

  Des groupes finis connus dans le Rubik's cube
  Sous-groupe des carrés (squares subgroup)
  Sous-groupe <h2, d2>
  Sous-groupes du sous-groupe des carrés
  Sous-groupe <a, d>
  Le groupe "sandwich" (slice group)
  Le groupe "sandwich au carré" (slice squared group)
  Ordre de quelques sous-groupes

Retour vers la page "Groupe du Rubik's cube"       



Des groupes finis connus dans le groupe du Rubik's cube  
Le groupe du Rubik's cube est un exemple de groupe fini dont l'ordre est relativement grand et qui n'est pas un groupe générique ( groupes symétriques Snet groupes alternés An, groupes diédraux Dn).
Il a de multiples sous-groupes et possède à ce titre quelques propriétés intéressantes.

Tout groupe d'ordre inférieur à 13 est isomorphe à un sous-groupe de G.
Z/13Z (le groupe cyclique d'ordre 13) n'est pas isomorphe à un sous-groupe de G.

Tout groupe non-abélien d'ordre inférieur à 26 est isomorphe à un sous-groupe de G.
D26 (le groupe diédral d'ordre 26) n'est pas isomorphe à un sous-groupe de G

Il existe une représentation du groupe des quaternions dans G.
Q* =< 1, m435, m706, m707, m710> est isomorphe au groupe des quaternions

Avec les notations suivantes :
MR = "middle right quarter turn" = 1/4 de tour de la tranche de droite
(celle qui coupe verticalement la face avant) dans le sens des aiguilles d'une montre
lorsqu'on regarde la face de droite.
m435 = a2 (MR)' 2 (MR)2 h' (MR)2 a2(MR)2 a2
m706 = a2 (MR) h' (MR)' h' (MR) H (MR)' h a2
m707 = p' a2 d' h' (MR) h d h (MR)' h' a2 p
m710 = a h2 a' h' g' p' h2p h g

  Retour vers le haut de la page


Sous-groupe des carrés (squares subgroup)
Le sous-groupe des carrés (squares subgroup) est le groupe engendré par les demi-tours des faces.

On note Sq = <a2, p2, g2, d2, h2, d2> , le sous-groupe des carrés.

card ( Sq ) = 213 x 34 = 663 552
et
diamètre ( Sq ) =15

Remarque : Sq est un groupe résoluble.
Voir "Mathematics of the Rubik's cube" page 226

  Retour vers le haut de la page


Sous-groupe <h2, d2>
Une page complète sur ce sous-groupe, avec la démonstration et l'explication des isomorphismes, la table de Cayley, les classes de conjugaison, les sous-groupes de <h2, d2>

On note H2D2 = <h2, d2>.

Un produit semi-direct
H2D2 Z / 6Z Z / 2Z D6
représente le produit semi-direct.

Un produit direct
H2D2 S3 x Z / 2Z

  Retour vers le haut de la page


Sous-groupe du sous-groupe des carrés
Sous-groupe <h2d2>

<h2 d2> est un groupe cyclique, donc abélien, d'ordre 6
<h2, d2> Z / 6Z

Remarque : la manoeuvre (h2 d2)3 est "la manoeuvre des six"

Sous-groupe <h2, d2>
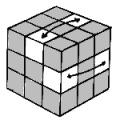
card( <h2, d2> ) = 12   et    diamètre( <h2, d2> ) = 6

  Voir les détails et la démonstration de ce résultat

Sous-groupe <h2, d2, g2>
card( <h2, d2, g2> ) = 96   et    diamètre( <h2, d2, g2> ) = 10

Sous-groupe <h2, d2, g2, b2>
card( <h2, d2, g2, b2> ) = 192   et    diamètre( <h2, d2, g2, b2> ) = 8

Sous-groupe <h2, d2, a2>
card( <h2, d2, a2> ) = 2592   et    diamètre( <h2, d2, a2> ) = 14


  Retour vers le haut de la page


Sous-groupe <a, d>

D.Singmaster a démontré que
<a, d> S7 x PGL2 ( F5 )

(Démonstration à voir dans "Mathematics of the Rubik's cube")

card ( <a, d> ) = 7! x 120 = 73 483 200

Remarque :
a est un élément d'ordre 4, d est un élément d'ordre 4 et ad est un élément d'ordre 105.
Ceci montre bien quelle peut-être la complexité d'un groupe engendré par deux éléments qui sont, a priori, peu complexes.
D'ailleurs, le groupe du Rubik's cube est engendé par deux éléments...

Algorithme de Dieu ( <a, d> ) = 25


  Retour vers le haut de la page


Le groupe sandwich (slice group)
Le groupe sandwich (slice group) est le sous-groupe engendré par les manoeuvres ap', dg' et hb'.
Avec cette définition, le groupe sandwich est un sous-groupe de G, le groupe du Rubik's cube, et les centres des faces sont fixes.
Mais on a coutume, à un isomorphisme près, de définir ce groupe d'une autre manière, qui est plus naturelle visuellement, à partir des rotations des tranches du milieu.

Le groupe sandwich est le sous-groupe engendré par les rotations des tranches du milieu (middle slice).

Attention ! Ces rotations font bouger les centres des faces !
Ce groupe n'est pas un sous-groupe de G qui est un sous-groupe de S48 et qui laisse fixes les centres des faces. Le groupe sandwich ainsi défini est un sous-groupe de S54 et est isomorphe à un sous-groupe de G (celui défini précédemment par <ap', dg', hb'>) .

 Une tranche du milieu est l'ensemble des huit petits cubes qui sont compris entre deux faces parallèles (la tranche de jambon du sandwich ...).
Il y a trois tranches : la tranche de devant (MF : middle front), la tranche de droite (MR : middle right) et la tranche de dessus (MU : middle up).

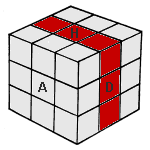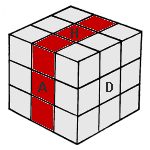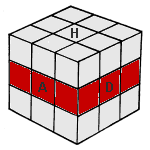MF : middle front MR : middle right MU : middle up


On note par le nom de la tranche (MR, MF, MU) la rotation d'un quart de tour de la tranche (les deux faces extérieures parallèles étant fixes) dans le sens des aiguilles d'une montre lorsqu'on regarde la face dont la tranche tire son nom (face Avant, Droite, Haut).

On note Sa = <MR, MF, MU> , le groupe sandwich.

card Sa = 768

Avec les notations précédentes,
fS : g dans G --> gS dans S8        où gS est la permutation des CS induite par g
fA : g dans G --> gA dans S12        où gA est la permutation des CA induite par g

Sa = { g dans G; fS(g) ( = gS) = 1 , sgn (gA) = 1 et xg = ( 0, ... , 0)}

ce qui signifie que les éléments de Sa sont les permutations du Rubik's cube qui laissent fixes les CS, qui effectue une permutation paire sur les CA et qui ne change pas l'orientation des CA.

Le diamètre de Sa est 20.


  Retour vers le haut de la page


Le groupe "sandwich au carré" (slice squared group)
Le groupe "sandwich au carré" (slice squared group) est le sous-groupe engendré par les rotations des tranches du milieu (" middle slice") de deux quarts de tour ... c'est-à-dire d'un demi-tour.

On note Sc = < MR2, MF2, MU2 >.

Le groupe "sandwich au carré" Sc est abélien

Sc ( Z / 2Z )3
et est donc d'ordre 8

  Voir les détails et la démonstration de ce résultat  (Table de Cayley du groupe, passage au quotient).


Le diamètre de Sc est 3.


  Retour vers le haut de la page


Ordre de quelques sous-groupes
   Stabilisateur d'une face
   Stabilisateur des cubes-sommets
   Stabilisateur des cubes-arêtes
   Le groupe anti-sandwich (antislice group)
   Ordres d'autres sous-groupes


  Stabilisateur d'une face
Le stabilisateur d'une face est le groupe des permutations du cube laissant fixe les cube d'une face.

Le cardinal du sous-groupe stabilisateur d'une face est 8! x 4 x 3 27 x 33 = 1 672 151 040

Cela signifie qu'il n'y a plus qu'environ 1,6 milliard de situations possibles du cube lorsqu'une face est faite !!

Explication :
8! est le nombre de positions possibles des huit CA mobiles (quatre sont fixés sur la face invariante).
Une fois les CA placés, il reste à placer quatre CS.
Mais une fois deux de ces CS placés, la place des deux autres est déterminée (on ne peut pas permuter uniquement deux pièces du cube). D'où la multiplication par 4 x 3.
Ensuite l'orientation des CA donne une multiplication par 27 (l'orientation de sept des huit CA implique celle du huitième) et celle des CS donne une multiplication par 33 (l'orientation de trois des quatre CS implique celle du quatrième).

   Retour au menu "Ordre de quelques sous-groupes"        Retour vers le haut de la page

  Stabilisateur des cubes-sommets
Le stabilisateur des cubes-sommets est le groupe des permutations du cube laissant fixe les cubes-sommets (CS), c'est-à-dire qui n'affectent que les cubes-arêtes (CA).

On note :
Le cardinal du sous-groupe stabilisateur des cubes-sommets est : card HA = 980 995 276 800


   Retour au menu "Ordre de quelques sous-groupes"        Retour vers le haut de la page

  Stabilisateur des cubes-arêtes
Le stabilisateur des cubes-arêtes est le groupe des permutations du cube laissant fixe les cubes-arêtes (CA), c'est-à-dire qui n'affectent que les cubes-sommets (CS).

On note :
Le cardinal du sous-groupe stabilisateur des cubes-arêtes est : card HS = 88 179 840


L'algorithme de Dieu est connu pour ce sous-groupe : il est de 14 mouvements avec uniquement les quarts de tours de faces et de 11 mouvements en comptant les demi-tours comme un seul mouvement.

Remarque (rappel) :
card( G ) =card( HS ) x card( HA ) / 2

En effet, G n'est pas isomorphe au produit direct HA x HS mais à un quotient d'indice 2.

   Retour au menu "Ordre de quelques sous-groupes"        Retour vers le haut de la page

  Le groupe anti-sandwich (antislice group)
Le groupe "antislice" est le groupe engendré par les éléments dg, ap et hb.
On note AS = <dg, ap, hb> , le groupe anti-sandwich.

card (AS) = 6144

   Retour au menu "Ordre de quelques sous-groupes"        Retour vers le haut de la page

  Ordres d'autres sous-groupes
| <h, a, d> | = 170 659 735 142 400
| <h, d2, g2> | = 212 34 52 7 = 58 060 800
| <h2, d, g2> | = 212 34 52 7 = 58 060 800
| <h, d2, a2> | = 28 35 52 7 = 10 886 400
| <h, d2, g2, b2> | = 213 34 52 7 = 116 121 600
| <h, d2, g2, b> | = 215 34 52 72 = 3 251 404 800

   Retour au menu "Ordre de quelques sous-groupes"        Retour vers le haut de la page