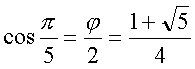 , c'est-à-dire
, c'est-à-dire 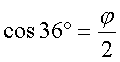
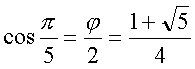 , c'est-à-dire
, c'est-à-dire 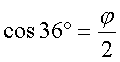
Le polynome X5 – 1 a pour racines les racines 5èmes de l'unité, c'est-à-dire les nombres ![]() pour k = 0, 1, 2, 3 et 4 ou bien k = 0, 1, -1, 2 et -2.
pour k = 0, 1, 2, 3 et 4 ou bien k = 0, 1, -1, 2 et -2.
| On a donc | |
| Mais on a aussi | |
| D'où l'égalité : | |
| En posant |
a et b sont donc solutions de l'équation ![]() qui a pour solutions
qui a pour solutions ![]() et
et ![]() .
.
D'autre part, on obtient en développant
| et |
| donc | et | ||
| On obtient alors : | et |
On cherche maintenant la valeur de ![]() .
.
On utilise ![]() et on obtient
et on obtient ![]() d'où
d'où ![]() .
.
Or, ![]() , donc
, donc 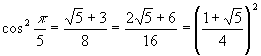 .
.
Finalement, on trouve